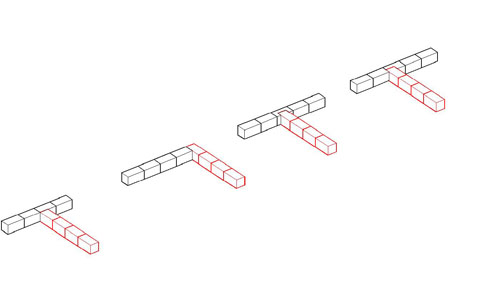
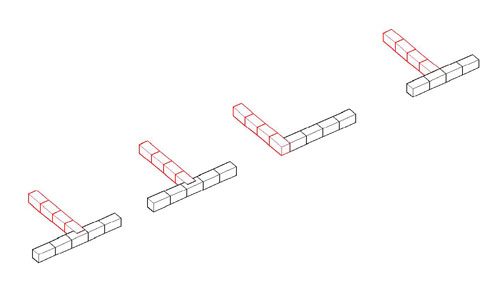
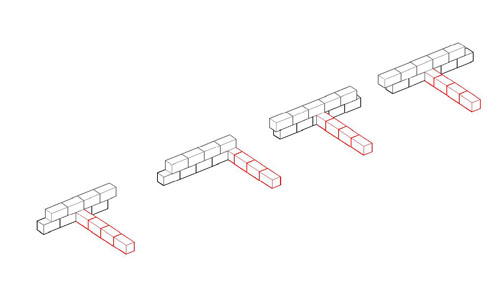
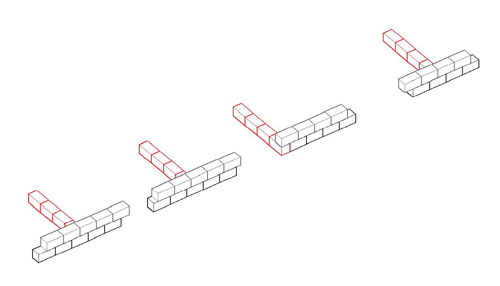
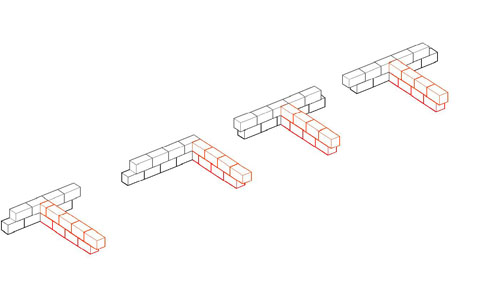
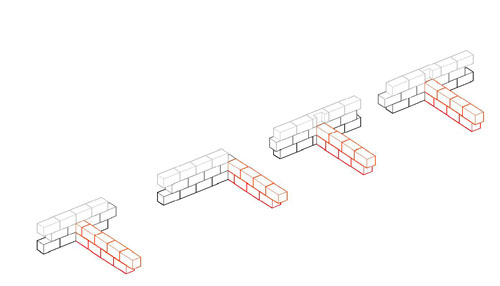
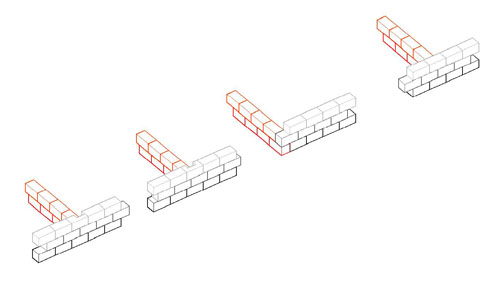
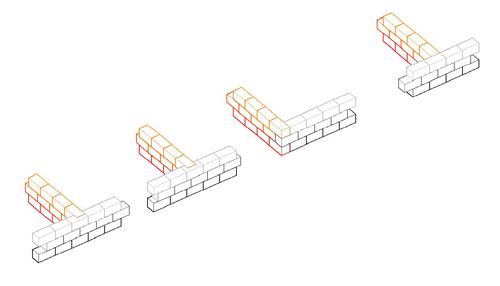
Several things have combined to make me suspect that the key to understanding the design of Greek monumental buildings may be the nature of the module of design, and I am thinking that the module is the block length, rather than some measured length. For that reason, the following is important. It shows the ways walls may intersect, and of particular importance is the ways they intersect without seeming to interrupt the block pattern on the continuing wall. That is, the exterior of a Greek temple does not show the presence of a cross-wall even when such a cross-wall does exist. The intersection patterns shown here permit that observed fact, but only one form of the intersection also permits the block pattern on the cross-wall and the block pattern on the inside face of the continuing wall to remain constant as well. That is the intersection pattern that has the cross-wall strike the continuing wall on a joint, not in the middle of a block (far right on the left-hand drawings, far left on the right-hand drawings.

If, as I now suspect, the block length is the module, the one form of intersection should be the norm. Unfortunately, we cannot tell from simple observation whether that pattern is the one in use on any given, standing wall.

Here are the drawings that illustrate the wall intersection possibilities. Each is linked to a larger version if you are having trouble figuring out the coursing and connections with these small drawings.