


 |
 |
 |

Important notice: The CSA web site was re-designed in August of 2010. Some documents then available were considered complete and static; so they were not included in the re-design and were not updated. This is one of those documents. Information about dates of posting and revision remains here, but there will be no revision of any kind after August, 2010.
Parts of the following discussion may seem elementary to some readers, but the issues discussed -- and the implications regarding the proper use of CAD -- are crucial to all who use CAD programs.
The term precision, when regarding a measurement, refers to the exactitude with which a measurement is made, not the correctness of the measurement. That is, a precise measurement is one made to a fine level of discrimination, for example, to the nearest millimeter or to the nearest sixty-fourth of an inch. A less precise measurement might be made only to the nearest centimeter or the nearest thirty-second of an inch. Regardless of the precision of a measurement, any given measurement may be accurate or inaccurate. A measurement of 1.2345 m. is precise, but the precision does not guarantee accuracy.
The term significant digits is related to the idea of precision. The term refers to the number of meaningful digits in a number, in this context, a measurement. Thus, a measurement of a block of wood known to be 2.01034 m. long, expressed with two significant digits, is 2.0 m.; if expressed with three significant digits, the measurement would be 2.01 m.
There is a direct relationship between precision and significant digits. Measurements are normally expressed with a number of significant digits corresponding to the precision with which the measurement was taken. Thus, assuming that we are able to measure that block of wood to the tenth of a millimeter, using a micrometer, we would show it as being 2.0103 m. long. If, however, we could only measure to the nearest millimeter with a steel tape, the measurement would be 2.010 m. The trailing zero may seem to offer no information, but, in fact, it shows that the measurement was made to the nearest millimeter. The number 2.01 would, on the other hand, indicate that the measurement was made only to the nearest centimeter. (There are ways to indicate significant digits to the left of the decimal point, but they need not concern us. CAD models will not be built with such low precision. Of course, leading, as opposed to trailing, zeros are not considered significant.)
The micrometer measurement could not be properly expressed as 2.010340, because the trailing zero would imply that the measurement had been made to the nearest thousandth of a millimeter. Nor could the measurement with a steel tape be properly expressed as 2.0100 m.
Precision is indicated on drawings through the use of significant digits. Where dimensions are shown, precision is clear, because all digits are assumed to be significant. (Note that this equivalence of significant digits and precision is one of the advantages of the metric system. A measurement of 1 1/2 inches may mean that the measurement was only made to the nearest half inch. However, the measurement could have been made to the nearest sixty-fourth of an inch. Using the metric system as a guide, one might expect to have 1 1/2 inches expressed as 1 32/64 if the measurement had been made to the nearest sixty-fourth of an inch, but that is not the custom with fractional measurements. In the English system, the designation 1 1/2 ±1/128 would be used instead.)
When dimensions are not shown on a drawing, there is no explicit showing of precision. Instead, any measurement can be retrieved by making measurements on the drawing and applying the scale factor. In such cases, the scale of the drawing is the more important limiting factor in retrieval precision, regardless of measurement precision. Retrieved precision is limited by the double problem of scale -- the accuracy with which the draftsman, working at reduced scale, can produce a line of appropriate length and the accuracy with which a user can measure and scale up a line on the drawing. Thus a 1:100 drawing can probably provide precision to the nearest tenth of a meter at best -- assuming original measurement to the mm. and drafting precision plus paper measurement keeping precision to the nearest mm.
CAD models present a different setting for determining precision. All points are specified in a 3D Cartesian grid system, and dimensions are calculated from those point locations. Dimensions need not be included in drawings, because they can be obtained via the program's query system for any points in a model; dimensions are calculated from point coordinate data on demand. The precision of the point locations in the model (and therefore of all measurements based thereon) depends on the CAD system and some underlying variables. The precision is, however, the same for all points in any given model; trailing zeros are automatically added as necessary or additional digits truncated to achieve uniform precision. Apparent precision -- the number of decimal places shown on screen -- can be changed. Users may, on most CAD systems, determine the number of decimal places shown in response to a query, whether for point locations or for dimensions. However, all point locations and dimensions in a given model will be displayed with the same apparent precision -- the same number of decimal places. There is no way to instruct the system to display some dimensions or point locations with one level of precision and others with a different level of precision. Thus, the number of decimal places shown is determined by the CAD system (and by the user, if the user changes the default value), not be the precision of any specific measurement. Since the number of decimal places may be unrelated to real precision, false precision -- through the display of inappropriate trailing zeros -- may often be indicated.
Accuracy is different from precision. An accurate measurement is simply a measurement made correctly for the level of precision used. That is, a measurement made at a low level of precision should be as accurate but not as precise as a measurement taken at a very high level of precision. Measuring the block of wood mentioned above with most metal tape measures would permit us to measure to the nearest millimeter; a measurement of 2.010 m., therefore, would be accurate, though not as precise as the measurement made with a micrometer -- 2.01034 m. By the same token, a measurement taken with a cloth tape only marked in centimeters would be 2.01, and that would be accurate as well, though less precise still.
It is important to consider how to ensure accuracy, whatever the level of precision, since accuracy is obviously essential for any project. There are two principal ways to try to ensure that measurements are accurate. One, instruments can be checked and calibrated (or taken out of service) to make certain that there is no error introduced by measuring instruments. Even tape measures can be tested against a standard. Two, measurements can be taken more than one time -- possibly by a different person -- to be sure that the results are consistent. A repeatable measurement should be a good one if the instruments have been checked and the personnel properly trained.1
Making certain that measurements are accurate -- again, regardless of the precision sought -- should involve both calibration and checking of repeatability. Calibration tests the instruments; repeatability tests personnel and procedures. This is not the proper place to discuss the ways to calibrate instruments or to check for consistent, repeatable results, but accuracy must obviously be assured, and project directors must develop schedules for calibration as well as mechanisms to train and test personnel and procedures, with the latter done on a scheduled basis. One caution is warranted. Measuring seems simple; it is easy to assume that instruction is not needed. However, accuracy is simply too important to be left to personnel without good training.
When obtaining survey data or basing new points on existing ones, it is important to recognize the impact of precision on accuracy. Calculations involving multiple numbers cannot generate new numbers with more precision than the least precise number. For instance, a point known to be 1.2345 m. due east of another point defined by the coordinates x=1.23,y=2.45, and z=1.56 lies at x=0, y=2.45, and z=1.56 -- not at x=-.0045, y=2.45, and z=1.56. The new point cannot be more precise than the point upon which it is based; therefore, the second set of point coordinates would properly be considered inaccurate, not simply too precise. It tells a user something that is not actually known to be true.
This problem of unwarranted precision can be very significant, both because it is so easy to ignore and because many modern measuring instruments -- especially electronic ones with digital readouts -- imply precision that is not real. If, for example, an electronic distance-measuring device measures the distance from its location to a specified point, it may return a number such as 10.2343 m. The manual, however, may explain that the device is only accurate to the nearest mm., in which case the true distance is 10 .234 m. despite the unwarranted precision shown in the display.
Anyone doing survey work -- whether for CAD or not -- should be aware of this relationship between accuracy and precision and take appropriate steps to insure that the precision recorded falls within the range of the measuring system used to obtain them. That will, in practice, probably require users to round off numbers provided by some instruments.
The level of precision used in a given project is not a matter of training but of deciding, based on the nature of the project, what level of precision is appropriate. CAD systems are capable of recording virtually any level of precision; so the decision is not limited by the capabilities of the technology.
Designers of computer chips must work in measurements as small as hundredths of microns. For archaeologists and architectural historians, fortunately, measuring something to the nearest millimeter is normally the highest level of precision required. Even within the humanities, however, different projects require different levels of precision, and the nature of the project should determine the necessary precision.
Working in Pompeii on the remains of Roman concrete -- walls without the once-present veneer of stucco or marble -- requires precision to the nearest centimeter, but not to the nearest millimeter. The higher level of precision is not required, since the important, planned dimensions of the buildings -- measurements to the finished surfaces -- do not survive. The concrete wall cores that do survive were not -- and did not need to be -- constructed to tight tolerances; measuring with great precision therefore provides no useful information.
Similarly, centimeter-level precision is adequate for most architecture and for carpentry constructions, since that level of precision is at least as high as was expected for construction. Archaeological recording probably does not require millimeter-level precision either, although archaeologists are inclined to measure with greater precision than might be required. They are cognizant of the fact that the destructive nature of archaeological excavation prevents remeasuring; so precision seems warranted.
Ancient cut-stone architecture that does not involve mortar, on the other hand, requires a higher level of precision, because the absence of mortar and the unforgiving, inelastic nature of stone raises the precision required in construction to a higher level. Where the level of precision required in construction is so high, the precision of measurement must also be high. In general, of course, that is the rule; high levels of precision in construction and design create a need for high levels of precision in measuring the finished product. Lower levels of precision in construction, on the other hand, call for lower levels of measurement precision. (Basing precision on the nature of the project is not the most common way to determine measurement precision when paper drawings are used. For paper drawings a more practical approach is appropriate, matching precision to drawing scale so that the most precise measurements can be expressed in a drawing at the largest scale to be used. That is, knowing the largest scale at which project drawings would be made, a scholar would measure to the level of precision required by those drawings. In fact, the publication of English Heritage on CAD, The Presentation of Historic Building Survey in CAD p. 3, suggests that survey precision will be affected by the scale(s) at which surveyors expect drawings to be produced. That is certainly the case when surveyors are attuned to hand-drawing methods rather than CAD. (The publication is undated. Contributors are Dave Andrews, Bill Blake, Nigel Fradgley, Sarah Lunnon, and Paul Roberts. It is available over the Web as two PDF files through the English Heritage site at http://www.english-heritage.org.uk-- apparently accessible only with Internet Explorer. Follow publication links to free publications to reach the download page.)
Useful precision for CAD models is also limited by the condition of the material being measured. An eroded or damaged stone, for instance, will present edges that are rough and irregular. In such cases, to what point does one measure? If one measures to a specific point with a high level of precision, is that meaningful if the point cannot be reliably located or defined? Similarly, even new brick may be sufficiently irregular as to provide no certain point for measurement. In these cases, measurement precision must be tempered with reality. It may be possible to measure to the nearest millimeter, but that may falsify the data by suggesting a kind of certainty that simply cannot be obtained.
As a high level of precision may not be appropriate for certain kinds of objects or structures, so very precise measurements may also serve no purpose. A battlefield survey, for instance, requires only a rather low level of precision. Similarly, very precisely locating individual artifacts within an excavation is of no value unless the entire outline of the artifact is to be surveyed with that high level of precision -- and may not be of use even then. It is not, after all, meaningful to locate a coin or a pot with a precise position unless one identifies the point on the coin or pot so located and the orientation of the coin or pot.
Although precise measurements are not always needed, modern survey methods make it easy to obtain very high levels of precision. As a result, there may be a temptation to seek the precision that is possible rather than the precision that is appropriate. Furthermore, certain kinds of survey work -- measurements from total station surveying instruments for example -- automatically yield measurements with high levels of precision.
The use of higher-than-appropriate precision can yield very misleading models. In the case of constructed or erected objects, the implication is that the original builders and craftsmen worked to very tight tolerances. The actual tolerances, however, are more likely to have been much looser. (A furniture maker once said he liked doing house carpentry on occasion, because the tolerances were so much greater than with furniture. Mistakes of a quarter or half an inch simply did not matter. Much smaller errors were consequential when making furniture.)
Surveying and measuring with mixed levels of precision -- as when using a total station, for instance, along with steel tape measures -- creates different problems, because a model may contain very precise measurements and survey locations intermixed with less precise ones. Unless the total station numbers are rounded before entry so that precision is the same throughout, differing levels of precision will exist in the same model, requiring that users have ways to determine which measurements or locations have been more or less precisely determined.
Since CAD systems cannot display differing levels of precision and may therefore indicate spurious levels of precision, documentation must accompany CAD models to explain the precision used. The documentation should explain how precisely the dimensions and data points were determined, and it should indicate how users can discriminate between more and less precise measurements if both are present. (For example, different layers might be used for different levels of precision.) In addition, the setting for display of decimal places, if it can be set within the model rather than the program, should be appropriate for the precision used in the measuring process. This notion of documenting CAD files is one to which we will return regularly. It cannot be overemphasized that a CAD file without documentation is far less useful than one with good documentation and may be of no use at all.
When using a total station, very precise measurements will result, whether precise measurements advance the goals of the project or not. When they do not, it may be preferable to transfer data to a CAD program after reducing the number of significant digits. (If numbers are rounded off, the rounding method should be consistent, and it should be made explicit in documentation. In addition, original data files should be retained at least until the completion of the project.)
There is an additional problem with mixed precision on a project. If a given point has been defined at one level of precision, no points surveyed on the basis of that point location can have a higher level of precision. Thus, a total station set up by sighting on a point surveyed with steel tapes cannot produce point coordinates more precise than to the level achieved with steel tapes, at best to the nearest mm. In such a case, however, any points surveyed from that total station position would have precise internal relationships, one to another. That is, the distances between points surveyed with the total station might be more precise than the coordinates of any single data point. Such complications require both care with survey methodology and careful documentation of the procedures followed. 2
How does one obtain the data for a CAD model? It would be very helpful if the data were commercially available in some computer format, but that is not the case. Most new buildings are designed with CAD systems, and, as a consequence, CAD models of them may be available in the future (although those models will be "as-planned" not "as-built" versions of the structures). Otherwise, however, scholars must make their own models by surveying the structure(s) they wish to model or by using existing paper drawings.
Scholars needing 3D models will be particularly dependent on their own survey work. Existing drawings, when they do exist, are rarely adequate for making full 3D models.
The first issue for the surveyor is whether the work is to be done in two or three dimensions and whether a wire-frame, surface, or solid model is to be created. (As pointed out earlier, most models will not be exclusively a wire-frame, surface, or solid model; nevertheless, most models will be predominately one or the other. The way the work is carried out will depend on that predominate mode.) One would set out to create a wire-frame model only if there were no expectation of using the model for 3D viewing; a complex 3D model is simply too difficult to "read" if presented as an axonometric or perspective drawing in wire-frame mode. Thus, a wire-frame model presumes the use of plan views only. (A wire-frame model may be fully three-dimensional in the sense that the lines are all properly arranged in 3D space; that preserves all survey information if elevations were recorded. Nevertheless, if such a model is only used in plan view, its three-dimensionality is not apparent.) An archaeological site plan or a plan of the standing remains of a mostly-destroyed historic building might be treated as a plan only; a wire frame model would be appropriate in such cases, whether changing elevations are included or not. Figure 1, for instance, is a plan view of the older propylon, and the fact that various lines lie at different elevations and/or have differing elevations at their beginning and end points is neither relevant nor apparent in the plan view.

Figure 1 - A plan view of a portion of the older propylon on the Athenian Acropolis.
If the final result of a project is to be plan views or elevations, with no intention to seek a three-dimensional model, it may not even be necessary to survey three-dimensionally. An archaeological plan or remains of a mostly-destroyed building might be surveyed without recording the elevations of the survey points. Though complicated by the use of layers and potentially more precise than traditional drawings, such models could appropriately be conceived from the outset as only two-dimensional; recording in three-dimensions might be considered unnecessary.
Whether to use a two- or three-dimensional approach depends on the nature of the material to be surveyed. There are also cost considerations, of course. Not only is it more time-consuming to gather enough data for a 3D model, it is more time-consuming to model in three dimensions. When complete, a 3D model is, however, more useful in the sense that it can supply a fuller sense of the object(s) modeled as well as more data points. A 3D model is also more likely to be useful for other purposes -- renderings, virtual reality presentations, and use in GIS data sets. As a result, the decision regarding 2D versus 3D work is an important one that should be made with full awareness of the superiority of the 3D model as well as the cost in time and funds.
The next issue of importance to the survey process is the one discussed above -- precision. Whether one believes that appropriate precision for the project is very high, very low, or somewhere in between, the choice must be made explicitly at the outset. Much will depend upon that choice.
If very high levels of precision are required, sophisticated surveying equipment may be the only choice. If more moderate levels of precision are to be set, then more traditional measuring processes will suffice.
The advantage of sophisticated surveying instruments -- total stations and their offspring -- lies in their ability to provide precision for long measurements as well as short ones. That is, a steel tape will provide excellent precision and accuracy for short dimensions, though the problems of full three-dimensionality make using a tape more difficult. Longer dimensions, however, inevitably introduce error due to sagging tapes, difficulties in measuring along oblique or curved surfaces, problems with making measurements along a vertical or, worse, a horizontal line, and so on. Determining longer dimensions by combining shorter ones creates different problems, since errors propagate.
Data precision is differently determined when the starting point is not a structure or excavation but drawings. When drawings represent the core data, the precision that can be retrieved from them determines the precision that can be achieved with the model. Scale is the most obvious limiting factor for drawings, but drawing quality will also affect precision.
There are several ways to accomplish a field survey. Each has strengths and weaknesses, and a useful comparison of some of the systems may be found in Surveying for Computer-Aided Drafting and Design -- Experiments in Three-Dimensional Techniques by H. Eiteljorg, II (http://www.csanet.org/inftech/srveybk.html). Another valuable resource is: David Andrews, Bill Blake, Mike Clowes and Kate Wilson, The Survey and Recording of Historic Buildings, Barabara Hurman and Mélanie Steiner, eds., Association of Archaeological Illustrators and Surveyors Technical Paper 12, 1995. Generally speaking, no single system will suffice for any project. Instead, some combination of survey approaches will be used.
II. 3.3.1 The Total Station: One of the most useful modern surveying instruments in the total station. A total station is an electronic transit with an electronic distance measuring device (EDM) and usually a data recorder. The electronic transit displays swing angles (deviation from north) and the angle above or below the horizontal. The EDM sends an infrared beam to a reflector that must be positioned at the point to be surveyed and uses timing algorithms to determine the distance to the reflector from the instrument. The data recorder records the position of the instrument, the swing angle, the elevation angle, and the distance to the target for each measurement. In addition, the data collector (and often the total station itself) can use simple trigonometric formulae to compute the position of a point surveyed from the known position of the total station and the data supplied -- swing angle, elevation angle, and distance to point.
Some total stations are now able to measure distance without a reflector. They are more expensive than the models that require a reflector, but prices have declined. These instruments cannot necessarily make a reading from any surface, since any surface to be read must reflect a significant portion of the light striking it. Therefore, even those using total stations that do not require a reflector will occasionally need a reflector, and some of the problems with reflectors will be encountered. Surveyors will need assistants to hold the reflectors -- and data points that are within reach of those assistants. See my CSA Newsletter articles concerning some of these physical problems of using total stations and reflectors -- "Pompeii in 1996" Vol. IX, No. 2; August, 1996 (http://csanet.org/newsletter/aug99/nl089608.html), "New Survey Aids" Vol. IX, No. 1; May, 1996 (http://csanet.org/newsletter/may96/nl059607.html), "New Total Station -- Surveying in Pompeii" Vol. VIII, No. 2; August, 1995 (http://csanet.org/newsletter/aug95/nl089506.html), and "Using a Total Station" Vol. VII, No. 2; August, 1994 (http://csanet.org/newsletter/aug94/nl089407.html).
Total stations can be purchased to operate at various levels of precision. The higher the precision, not surprisingly, the higher the cost. Some will measure angles to the nearest ten seconds, some to the nearest second, others in between. Some will measure distances to the nearest 5 millimeters, some to the nearest millimeter, and other in between (always with an additional potential error factor related to the distance of the measurement). The level of precision should be chosen to match the work being done, and some simple trigonometry will show what level of precision is required. For instance, assuming a one-second machine with a one-millimeter EDM, any measurement should be less than 2 mm. in error even if measuring from 100 meters away, still under 1 cm. at a kilometer distant. With a five-second machine and a three-millimeter EDM, the maximum error should be about 3 mm. at a measuring distance of 10 meters and less than 5 mm. at a measuring distance of 100 m. 3 Selecting the correct machine is a matter of matching the expected working distance and conditions, the precision required, the machine capabilities, and price. Of course, practical considerations such as available local service, familiarity with the brand, and so on may also be important. Finally, there will almost always be survey software included. The capabilities and limitations of that software should be examined.
Although many more data points can be gathered in in a given span of time with a total station than with any manual method of surveying, total stations offer more than speed of survey as advantages. The data can be directly transferred to a computer and into a CAD system, so the opportunities for error are greatly reduced; here again, speed is gained as well. The nature of the data transfer will be determined by the survey software included in the total station package.
There are various practical problems related to the use of the total station; most are dealt with in CSA Newsletter articles mentioned above. Some of the newer instruments may circumvent the problems discussed in those articles, but familiarity with the problems and solutions should aid in selecting an appropriate instrument.
Using a total station does not fully automate the data-gathering process. The points will be surveyed, and the coordinates can be transferred to a computer via cable and from there into a CAD model. However, the data consist of simply a numbered and annotated group of point coordinates. The operators must connect the points to make a useful CAD model. Therefore, sketches must be made on-site very much as they would be if one were taking standard tape measurements. Surveyed points must be noted so that the operators of the CAD system will know how to translate isolated data points into the surfaces, lines, arcs, and so on that are the CAD model.
II. 3.3.2 Total Stations with On-site Computers: It is possible to work with a total station connected directly to a computer rather than a data collector. The computer can serve simply as a data collector, in which case the system is not appreciably different from a simple total station. In other cases, however, the input from the total station goes directly into a CAD program as if typed from the keyboard. At the moment, such systems are available only for making wire-frame models, not surface- or solid-models, but, as is true for the computer world generally, things can be expected to change and to change often. For those who work in settings that would permit remaining connected to an electrical supply, such systems should be examined.
II. 3.3.3 Global Positioning System Receivers: Another high-tech surveying device is the GPS (global positioning system) receiver. Signals from satellites are received by the ground units, and calculations based on the signals can locate the receiver quite precisely. Although individual units can be used to provide better than meter-level precision, multiple units working in tandem (one stationary to serve as a control) may increase the precision to within 10 cm. or so. The precision figures cited by manufacturers are nearly always for x and y coordinates -- easting and northing in surveying terminology -- not elevation. In general GPS units cannot match their x- and y-precision when providing elevations.)
With their lower level of precision, compared to total stations, GPS units are excellent for landscape work, field survey, and other kinds of survey work that does not require more precise results. As with total stations, various levels of precision are available. Whatever the precision, GPS units offer the same advantages in terms of speed of data gathering and simplicity of data transfer. Indeed, for landscape survey using a GPS is faster by far then using a total station.
II. 3.3.4 Traditional Measurement: If dimensions are to be made with tapes, plane tables, and the like, elevations must be included with all measurements. All data points in a 3D model, of course, must have an elevation. Triangulation becomes especially difficult when 3D points are required, and it is probably best to measure points in two steps, as normally done for plans, one to locate the position in plan view only, and another to determine elevation.
II. 3.3.5 Photogrammetry: Photographs can also be used to generate digital data. The easiest data to obtain from photographs are details from flat surfaces, e.g., the pattern of a mosaic floor or the cracks on a wall. A single photograph can be placed on a digitizer and traced, just as if it were a drawing (see below), even if the photo was taken at an angle oblique to the surface in question. (Admittedly the process is more complex than with a drawing, but it is not particularly difficult.) This process works only for details on flat surfaces, and all data points are placed on a single plane; they are essentially 2D locations. The system performs a rather simple mathematical process called a plane transformation.
Photogrammetry can obtain fully 3D data from photographs, but multiple images are then required. Traditional photogrammetry requires photographs in pairs with a known distance between the two camera positions and very sophisticated equipment. Newer methods, often called close-range photogrammetry or desktop photogrammetry, use three or more photographs and various computer algorithms to locate positions of points that can be identified in multiple photographs. The latest of such programs use digital images rather than photographic prints, but the resolution of digital images is low enough that those methods are not likely to produce the levels of precision generally desired. (here again, changing technology will have an impact. Digital cameras have rapidly improved, in terms of resolution, and may be adequate for photogrammetry in time.)
II. 3.3.6 Aerial Photography: Photographs from the air may be used to gather information, either plan-level information or elevations. Aerial photographs can provide information for landscape survey more efficiently than any other method, though usually not with very high levels of precision. A publication has been prepared as part of the Arts and Humanities Data Service's Guide to Good Practice series and should be consulted for more information on the use of aerial photography -- Archiving Aerial Photography and Remote Sensing Data: A Guide to Good Practice, by Robert Bewley, Danny Donoghue, Vince Gaffney, Martijn van Leusen, and Alicia Wise (http://ads.ahds.ac.uk/project/goodguides/apandrs/).
II. 3.3.7 Direct object scanning: Scanning objects (as opposed to scanning drawings thereof, discussed below) is technically possible. Many kinds of of devices -- mechanical, magnetic, and optical -- are available. Such devices tend to be expensive. Those suitable for survey of larger objects (even including structures) are heavily automated, not only making them very expensive but often making the resulting models much more complex than necessary. That is, excess data points are collected, depending on the grid applied to the structure, and software must remove those not required -- for instance, those not at the edge of a large, flat surface. The process of removing the excess points -- called decimation -- is still improving. In addition, separating the various points for the sake of CAD layers is very difficult when the points are so numerous and are not tied to specified points in the real world.
The data points surveyed in an automated system depend on a pre-set grid rather than logical choices of required points. Thus, the points surveyed are not necessarily the ones a scholar would choose; they are the ones the machine has selected, as directed by the spacing of the grid applied.
Whether survey data comes from a total station or hand measuring techniques, 3D CAD models require many more data points than traditional paper drawings. A door or window opening, for instance, will have at least twice as many points for a 3D model as for a plan, see Figure 2. Even when a wall can be assumed to be vertical, the meeting of wall and ceiling must be surveyed as carefully as the meeting of wall and floor. Of course, details within the structure would add more data points for survey.
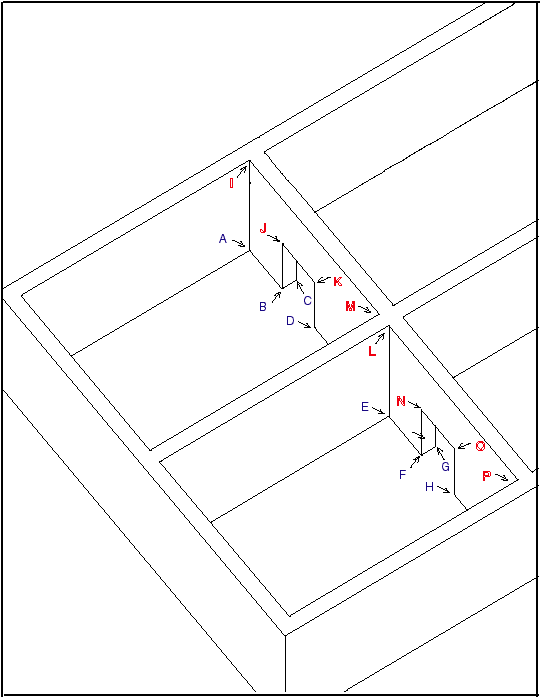
Figure 2. Survey points visible on the walls roughly in the center of this drawing have been marked. Points A through H (blue) would be needed for a plan-only, 2D survey. Points I through P (red) would also be needed for a 3D survey.
This added complexity of making a 3D model requires some familiarity with 3D modeling before beginning survey work. Otherwise, the tendency to take points for plans rather than full models is likely to be irresistible. Even with model-making experience, it is very desirable to transfer data recorded in the field into a 3D model quickly so that the data points needed but not taken can still be gathered on the next trip to the site.
If one has available plans and/or elevation drawings, it is possible to use them to enter data in a CAD system in either of three ways. One, the information from the drawings can be used to provide the dimensions and locations of geometric shapes. In that case, the process is not different from the process used to make a model from standard hand measurements, and, assuming all dimensions are available, a proper 3D model can be constructed. Two, the paper drawings can be scanned, but, in that case, the model will consist only of 2D information, like the paper originals, rather than 3D models. Such drawings can also be traced, but the result will, here again, be two-dimensional. Neither scanning nor tracing is a completely automatic process.
If the drawings are scanned, the result is a raster image rather than a vector image [see Introduction and CSA Newsletter article on this matter, Susan C. Jones, "Raster and Vector Images -- An Important Difference," Vol X, No. 1; Spring, 1997 (http://csanet.org/newsletter/spring97/nl059707.html)]. To use the raster image effectively, it must be made into a vector image. There are automatic tracing programs that purport to do this, but they have a limited range of usefulness. Lines that cross one another often, for instance, confuse the programs since it is difficult to write software that can determine which direction to follow at an intersection. Other problems may arise due to paper shrinkage, scaling, and the like. There are many such programs available; some trials should be undertaken with the drawings at hand before investing in one, and, given the rate of advance in software design, revisiting software on a periodic basis is worth while.
It is possible to scan a drawing, view it on screen, and trace the lines on screen; the traced lines become new information for the CAD program. Of course, one may also combine that tracing process with automatic line-following programs.
A better way to digitize plans is to trace them on a digitizer, an electronic drafting board that provides data input to a computer in place of a mouse. Large digitizers are available so that even drawings of considerable size can be traced easily. (Drawings of any size can be traced and properly oriented, working on a portion of the whole at a time, even on small digitizing tablets. However, larger ones save time when dealing with large drawings.) Scale, position, and orientation are established before tracing, and the draftsman has complete control over the tracing process. As a result, some, including the author, believe this to be the preferred process for digitizing existing drawings.
It is possible to use plans and elevations together to create 3D effects and, with some patience, 3D models. If a plan view is traced, for instance, the elevation can also be traced -- as an elevation starting on the proper points on the plan and placed on a vertical plane. Of course, adjustments will be necessary to accommodate the deviations from simple, planar drawings, but such adjustments are possible in some, if not all, cases.
Scanning and digitizing can be made much more accurate and precise if dimensions are available on the drawings -- as, for instance, with architectural drawings of a structure. Then the scanned or digitized figures can be altered to match dimensions. Indeed, it should be possible to build a superb CAD model from architectural drawings. It must be remembered, however, that such a model is a digital version of the structure as it was designed, not as it was built.
There are other systems for surveying -- sonic probes, for instance -- and new ones turn up regularly. Generally speaking, however, the systems already discussed -- total stations, GPS, hand measuring, photogrammetry, aerial photography, and digitizing -- are the ones to be prepared to use.
Any data source that consists of lists of point coordinates can be altered in other computer programs. In many cases, the alteration can be enormously helpful. For instance, the data points defining a series of blocks, by corners, can be placed into a spreadsheet or database, and formulae can create CAD commands in the spreadsheet or database. The commands can then be pasted into a CAD program and executed as if typed at the command line. Not only can such processes save a great deal of time, they permit adjustments and changes without laborious re-entry of CAD commands. Examples of such processes -- using spreadsheets and AutoCAD® -- may be found in the CSA Newsletter: H. Eiteljorg, II, "A Spreadsheet as a CAD Aid -- Again," Vol. XIV, No. 2; Fall, 2001 (http://csanet.org/newsletter/fall01/nlf0105.html); H. Eiteljorg, II, "Using a Spreadsheet to Speed AutoCAD Data Entry," Vol. XIII, No. 1; Spring, 2000 (http://csanet.org/newsletter/spring00/nls0004.html); and A. Vranich and H. Eiteljorg, II, "Making A Silk Purse From The Proverbial Sow's Ear," Vol. X, No. 1: Spring, 1997 (http://csanet.org/newsletter/spring97/nl059711.html).
As is so often the case in the real world, scholars can rarely use one method of data gathering exclusively. Total stations, for instance, do not work well at very close range, and they are cumbersome to use for small details. GPS units and software are excellent for survey work but do not provide sufficient precision for the details of standing architecture or excavation trenches. Photogrammetry is difficult and expensive but excellent for details that can be seen well in photographs (though there are some important limits on the way the photographs should be taken). Tapes and traditional hand-measuring systems are slow and, in the long run, inefficient, but no expensive tools are required. (It may also be argued that the process of measuring by hand provides greater familiarity with the subject and enhances the likelihood that real understanding will be achieved.) Tracing or otherwise digitizing existing drawings provides only 2D data and limited precision, but that process allows existing data to be utilized. Each system has its drawbacks. Each has strengths. In the field the most efficient is probably the total station or the GPS. If one is starting with measured drawings, the most flexibility and the best control of accuracy can be obtained through digitizing (tracing) the drawings.
Data from total stations and GPS equipment should be checked periodically to be sure what level of precision and accuracy have been achieved. Checking obtained dimensions against standards or measured comparisons should provide adequate checks, assuming that working methods are properly specified and followed.
Determining precision with photogrammetry or plane transformations is more complicated. If possible, dimensions should be taken in the field to provide a check. Otherwise, the determining factors are the scales of the images and digitizing error, as with drawings. Experiments similar to the ones suggested (below) for paper drawings should help fix the level of precision for photogrammetry and plane transformations.
As precision used in field survey must be determined in advance, so limits on precision created by other methods of data capture must also be understood. With paper drawings, the scale and quality of a drawing will affect the maximum level of precision that can be retrieved. So will the skill of the draftsman. (A simple experiment can be used to determine the operating precision possible with a digitizer. If the operator sets up a scaled drawing for tracing and then selects the same point again and again, the average error can be determined, as well as the maximum error. Assuming that the drawing has been well made, one would expect achievable precision to be about double the maximum error found in the experiment, assuming draftsman error roughly matches the error of the digitizing process. Comparing dimensioned distances from the drawing and the CAD model should give even better estimates of achievable precision.)
All factors affecting precision should be fully and accurately documented, and the documentation should be included with the CAD file. Potential users must be able to examine such documentation if they are to understand the quality of the data.
Note 1: An experiment reported in Surveying for Computer-Aided Drafting and Design -- Experiments in Three-Dimensional Techniques by H. Eiteljorg, II, (http://www.csanet.org/inftech/srveybk.html; access date 12 June 2002) shows relevant findings. Thirty dimensions were taken, each of a short distance that permitted a single individual to hold both ends of a steel tape measure. The measurements were taken a second time (by the same person) and the results compared. The average discrepancy between measurements was less than 1 mm., but there was one instance of two measurements differing by 6 mm. Were longer measurements made, ones requiring two people, the results would most certainly have shown larger deviations between successive measurements. Larger deviations would probably have been found if two people had taken the same dimensions. Back to text.
Note 2: There is obviously a problem with error propagation in a mixed-precision environment. Each point location is based on measurement from some known point, but in such a mixed-precision environment the known points themselves may be defined with differing levels of precision. Thus, when measuring a new point, the precision of the base from which the measurement begins determines the maximum precision of the new point location. In fact, any point used as a base for further measurement is only as precisely determined as the least precise point in the chain of such base points leading back to the very beginning of the project. No survey process can yield a point location with more precision that the least precise point in the chain of base points. To repeat, care and documentation are critical. Back to text.
Note 3: Using the tangent of the maximum angular measurement error and the distance from total station to measured point provides a number for maximum position error in one direction. Since the same error can occur in both horizontal and vertical directions, one must then imagine a square with the real point at one corner and the maximum error at the opposite corner; the diagonal of the square would then provide the maximum error introduced by angular measurement. To the angular measurement error must be added the distance measurement error (this time using the diagonal of an imaginary rectangle). In any case, the potential error due to angular mis-measurement is very small when compared to the error that may occur in the distance measurement. Back to text.
| Continue to next chapter. | Go to glossary. | Go to Table of Contents. | Go to CSA home page. |